何度かこのブログでデータ圧縮(書庫やエンコードなど)について解説してきましました。
しかし、その詳しい仕組についてはまだ書いていません。実際、実践的なところは難しすぎるので私もよく分かっておらず、専門的なことまではわかりません。(プログラミングは今後しっかり勉強していきたいですね。)
ですが、漠然と「取り敢えずデータが少なくなるんだよ!」と言われても釈然としないでしょう。少なくとも、私は「元の情報を残したままデータを小さくするってどうやるんだろう?」と疑問を持ちました。
なので、この記事ではデータ圧縮の基礎部分でよく使われる「ハフマン符号化」について書いてみたいと思います。
情報数学のお話になりますが、概要だけならとても理解しやすいものなので、今回はこれをテーマにしてみます。データの圧縮とはどうゆうことなのか、その一端でも知りたい方はお付き合いください。
ついでに「なぜコンピューターは0と1で構成させているのか」「ビットとは」なども最初に補足として解説します。
この記事を書く動機
このブログは「パソコン初心者~中級者」を対象とした内容で書いていることが多いです。
ではなぜ、このような小難しい話を書こうと思ったのか。
私は、できる限り「仕組み」についても知ってもらいたいと思っています。もっとコンピューターを知って好きになってもらいたいです。また概要だけでも仕組みが分かれば、何か問題に出会った時でも根底部分から解決を試みることができるようになります。引き出しが多くなるわけですね。
そういった意味でも、初心者的な操作方法などとはかけ離れたことでも長々と今まで書いてきました。
今回もその流れです。データ圧縮について様々書いてきたので、圧縮技術の基礎となる「ハフマン符号」について、その概要を書いてみようと思い立ちました。
「ハフマン符号化」、なんか小難しそうに見えますが概要はそんなに難しいものではありません。比較的簡単な部類ですので、「なんでデータサイズを小さくできるのか」その一片でも知りたい方はお付き合いください。

コンピューターの基礎「すべての情報は 0 と 1 で構成される」
通常、一般的なコンピューターはすべて「電気」によって動いています。
コンピューター内の回路には電気が流れています。この電気の流れをコントロールすることでコンピューターは計算をしています。ここまでは一般的な常識範囲かと思います。
では、実際どのように電気が流れているのか。
実はかなり単純で、回路内は「電気が流れている状態(ON)」 or 「電気がながれていない状態(OFF)」の2つの状態しかありません。一見不便そうに見えますが、エラーを起こさない方法としては非常に優秀な方法なのです。
電流というのは、どんなに精密に作っても少なからず「ゆらぎ」、誤差のようなものが発生してしまいます。しかし、例えば電圧が「0V~5V」までなら「電気がながれていない状態(OFF)」、「6V~10V」までなら「電気が流れている状態(ON)」と仮に定義すれば、多少電圧が揺れ動いても正しく「ON」「OFF」を認識、切り替えることができます。このように誤差を吸収できる、つまり回路内のエラーを最小限に抑えることができるため、「ON」「OFF」の2つの状態で制御させています。
この「ON」「OFF」を「1」と「0」に対応させてやることですべての情報を操るのです。プログラム側で電流が流れれば「1」、流れなければ「0」と認識するようにすれば電気の流れを数値に変換して処理できるようになります。
このように、 0 と 1 (2進数)で数える方法を「2進法」といいます。私たちはよく「0~9」までの10進数を利用した「10進法」を使って生活に役立てますね。人間の手の指の数が合計で10本あるからという理由が一般的らしいです。(確証はないらしいですけど・・・)
2進法の計算方法
10進法ならば、みなさんも御存知の通り「9」まで数えたら2桁になって繰り上がり「10」となりますね。
2進法でも同じように「0」→「1」と数えたら2桁になり「10」となります。そこから「11」→「100」→「101」・・・のように数えていきます。10進数と違うのは繰り上がりのサイクルが早いだけで基本は同じです。
なので計算は以下の通りになります。Windows7以降の電卓ならば2進数の計算もできるので一度お試しを。
「スタートメニュー」→「アクセサリ」に標準の電卓があります。Windows8ならばスタート画面で「電卓」と入力すれば見つかります。
加法:1001 + 1101 = 10110 / 減法:1110 – 1001 = 101
文字とかはどうやって表現するの? - 符号化・復号化 –
さて、これで「0」と「1」に関しては表現できるようになりました。
では、2以上の数字や文字などはどう表現すればいいのでしょうか。気になりますよね。
コンピューターの回路は 0 と 1 の2つしか電気信号として回路内へ乗せられないので、すべての数字・文字を「0」と「1」で構成させてやらないといけません。そこで、世界共通の「対応表」が考えださせれました。
| 2進数 | 対応文字 |
|---|---|
| 0110000 | 0 |
| 0110001 | 1 |
| 0110010 | 2 |
| 0110011 | 3 |
| 0110100 | 4 |
| 2進数 | 対応文字 |
|---|---|
| 1000001 | A |
| 1000010 | B |
| 1000011 | C |
| 0111110 | > |
| 0111110 | ! |
尺の関係でかなり省いていますが、以上は「ASCⅡ」と呼ばれるコード対応表(文字コード)の一部です。
それぞれの文字がすべて2進数で表現できるようになっています。これをプログラムが辞書として使うように設計すれば、すべての文字が 0 と 1 で処理できるようになります。今回は「ASCⅡ」を例にしましたが、他にも用途によって「Shift_JIS」「UTF-8」などの文字コードがあり、それぞれ割り当てられている文字が異なります。
そして、これら0と1に変換されたデータを「符号」と呼び、符号にすることを「符号化」と呼びます。
逆に、符号化されたデータを元の記号に戻すことを「復号化」といいます。
ビット
ビット【bit】とは、コンピューターが扱えるデータの最小単位を示す言葉です。「binary digit」を略したものらしいです。
ここまで勉強してきた方ならばお分かりでしょう。コンピューターはすべて2進数でデータを処理するということは、これらがコンピューターにおける最小単位となります。「1bit」ならば、「1」または「0」というデータになります。
そして、一般的に「8bit = 1Byte(バイト)」と定義付けられています。これは昔、爆発的に広まったコンピューターが8bitを1Byteとして設計したから、という理由らしいです。(7bit=1Byteというコンピューターもありました。)
例えば、100KByte(キロバイト)のデータは80万bit、つまり80万個の 0 と 1 のデータで構成させていると言い換えることができます。コンピューターはこれだけの情報をいとも簡単に処理できる能力を持っているということですね。
ハフマン符号化
前知識を解説したところで、本編「ハフマン符号化」について書いていきます。
ハフマン符号とは
ハフマン符号化【Huffman coding】とは、1952年にDavid Albert Huffman氏(デビット・ハフマン)によって考案された、可逆圧縮の代表的アルゴリズムです。(アルゴリズム【Algorithm】:仕事をさせるための手順)
コンパクト符号という符号化の一種で、一意に復号可能な符号のうち平均符号長が他より小さい符号のことを言います。
一意とは、2つ以上の値が存在しないことです。つまり、復号する際に解釈の違いによって復号後の結果が異ならないということを意味します。平均符号長とは、名前の通り全体の符号長の平均です。符号化前の符号の平均の長さより、符号化後の平均の長さが短くなれば圧縮成功となります。
まとめると、コンパクト符号の一種であるハフマン符号は『復号後の結果はちゃんと元の符号に戻ることができ、かつ全体のデータ量を減らすことができる符号化』ということになります。各記号の出現確率を事前に求め、出現度の高い文字を短い符号で、出現率が低い文字を長い符号で表現することで、平均符号長を最小とする圧縮技術です。
JPEGやZIP (Deflate) などの圧縮フォーマットで使用されているところをみれば分かる通り、ハフマン符号は算術符号などと異なり特許の問題がありません。誰もが自由に使うことができます。
符号化の手順
ハフマン符号化をすると、元の符号よりも必ず短くなります。常に最適解を求めることができるのです。
では、どのように平均符号長を短くするのでしょうか。
では、データ「ADBCBABCBBCE」をハフマン符号化してみましょう。
まずは、このデータを0と1のみで表現できるように変換をします。通常は文字コードなどを元にして変換しますが、今回はわかりやすくするため独自に変換させます。A~Eの5文字が使われているので、これらすべてを0と1で表すために必要な最小の桁数は『2の2乗 < 5文字 < 2の3乗』、つまり3bitである3桁です。
| A | 000 |
| B | 001 |
| C | 010 |
| D | 011 |
| E | 100 |
このように、割り当てた符号の長さがすべて一定であるものを「固定長符号」といいます。
対応表ができたので、データをすべて0と1で表してみると、以下の通りになります。
(分かりやすくするためにスペースを入れていますが、本来は連続したデータになります。)
000 011 001 010 001 000 001 010 001 001 010 100
全36文字、つまり36bit=4.5Byteになります。
これが符号化前のデータ、つまり無圧縮状態のものです。これをいかにして短くするか、手順を追って解説します。
ハフマン符号化の性質上、まずデータ全体を対象に「各記号の出現頻度を調査する」必要があります。
先ほどのデータを出現頻度順にソート(並び替え)してみます。
| 文字 | 固定長符号 | 出現頻度 |
|---|---|---|
| B | 001 | 5 |
| C | 010 | 3 |
| A | 000 | 2 |
| D | 011 | 1 |
| E | 100 | 1 |
ここから「ハフマン木(Huffman tree)」と呼ばれる木構造(バイナリツリー)を作っていきます。
まず、頻出頻度の1番少ない記号と2番めに少ない記号を木の一番下に位置させます。同数のものがある場合は、どちらが先でもよいです。これが木の「葉」に相当するものです。そして、ふたつの出現数を足して「枝」で結び、ひとつ上に新しい「接点」を作ります。
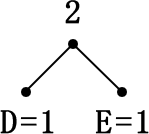
接点ができたら、その接点を含む他のすべての葉と接点をもう一度調査します。ただし、すでに合計された接点より前(下)の「葉」は調査対象から外します。まだ自身が合計されたことがない葉と接点、その値より上に新しい接点をまだ持ってない値、つまり”親を持っていない葉と接点”が再調査対象です。
先程の手順で「D」「E」が選ばれ合計されたので、この2つは調査対象外です。その時に合計された接点はまだ一度も合計されたことがないのでこちらは調査対象になります。新しくできた接点を仮に1つの記号として見なすと調査対象が分かりやすいです。
再調査した値の中から、再度最小の値と2番目に小さい値を持つ葉、あるいは接点を足し合わせてさらに新しい接点を作ります。次に選ばれるのは出現確率の値「2」を持つ記号「A」と、先程合計した「2」の値を持つ接点です。この2つを合計すると、新しい接点「4」ができます。ここからまた再調査が始まります。合計した接点「2」と、記号「A」「D」「E」はそれぞれ親の接点を持っているので再調査対象外になります。
以上のことを繰り返して、最後の値が取り出され接点と合計されたら木が完成となります。頂点(根節点)は記号の合計数になります。木ができたら、接点からでているそれぞれの枝に対して左右に 0 と 1 を割り振ってきます。どちらに 0 と 1 を割り振るかは任意です。
これで、それぞれの葉に対して一意のビットが割り当てられます。ハフマン木の完成です。
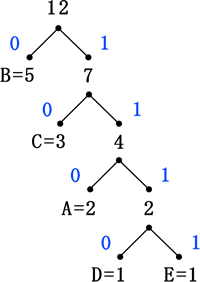
ハフマン木が完成したら、これを元に符号化をします。
各記号を符号化するには、根節点から符号化したい記号までのルートを辿り、通ったルート上にあるビットを順に記録します。例えば、Aを符号化したい場合は、以下のようなルートを辿ります。通ったルートから得られたビットは順に「1」「1」「0」なので、A=110という符号化が成り立ちます。
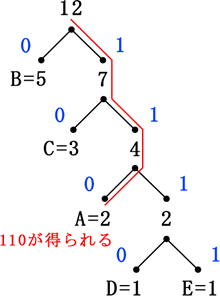
これをすべての記号に対して行い、すべて符号化させます。すると、最初の対応表とは異なる新しい対応表ができます。見ると分かる通り、出現数が多い記号ほど符号長は短くなり、出現数が少ない記号ほど符号長が長くなります。
このように、出現率によって符号の長さが変わる、つまり可変になることを「可変長符号」といいます。
| 文字 | 固定長符号 | 可変長符号 |
|---|---|---|
| B | 001 | 0 |
| C | 010 | 10 |
| A | 000 | 110 |
| D | 011 | 1110 |
| E | 100 | 1111 |
では、新しくできた対応表を元に新しく符号化してみます。
110 1110 0 10 0 110 0 10 0 0 10 1111
全25文字、つまり25bit=3.125Byteになりました。
最初に符号化した「36bit=4.5Byte」と比べると、約30%圧縮できたことになります。圧縮成功です。
では、本当にコンパクト符号なのかも調べるため、一緒に平均符号長も調べてみます。
平均符号長=それぞれの文字に対する(符号の長さ × 出現確率)の総和
符号化後の平均符号長=1×5/12 + 2×3/12 + 3×2/12 + 4×1/12 + 4×1/12 = 2.088888…
| 符号化前 | 000 011 001 010 001 000 001 010 001 001 010 100 | 全32bit 平均符号長 3bit |
| 符号化後 | 110 1110 0 10 0 110 0 10 0 0 10 1111 | 全25bit 平均符号長 約2.08bit |
この通り、平均符号長も短くなりましたのでコンパクト符号の条件に合いました。
すべてのパターンで短くなりうるかどうかはちゃんとした数学を使えば証明できますが、ここでは割愛します。
以上がハフマン符号化の大まかな手順になります。どうでしたか、意外に簡単なものかと思ったのではないでしょうか。
これがJEPG圧縮やZIP圧縮の基礎部分で使われている圧縮技術です。JPEG圧縮は不可逆圧縮なので、ハフマン符号化を適用する前に複雑なデータのカット処理が実行されていますが、その後は以上のようなハフマン符号化をしています。
ハフマン符号は、各記号の出現率の幅が広ければ広いほど圧縮率が高くなります。
今回解説した手順は、最初にすべての文字の出現頻度を調査してからハフマン木を作りました。このように、最初にデータの解析をして2度目に符号化を実行するハフマン符号化を「静的ハフマン符号 【Static Huffman coding】」といいます。汎用性が高く、多くのデータで実行できる圧縮方法です。ただ、全体の調査に1回、符号化に1回と最低でも2回のデータ走査が必要になるため、圧縮速度はそこまで早くないデメリットがあります。
一方、記号を1つ読み込む度にハフマン木を作り直し符号化を実行するハフマン符号化を「適応型ハフマン符号【動的ハフマン符号, Adaptive Huffman coding】 」といいます。こちらは最初の全体調査は不要なため、符号化も早くなるメリットがあります。ただ、データによっては必ずしも最小符号ができるわけではなく、若干圧縮率に劣ります。ですが、実用性に問題ができるほどではないので、一回で符号化が終わる利点を活かしてリアルタイムの符号化が必要なデータの場合には有効です。
ハフマン符号の復号
さて、符号化(エンコード)ができたら今度は復号(デコード)ができないといけません。
固定長符号の場合は、符号長が常に一定なので「最初から3bitずつ読んでいって、合致した記号に戻す」という作業をすれば一意の復号化ができます。
000011001010001000001010001001010100
固定長符号ならば、以上のようにスペースがない連続した符号でも、3bitずつ(固定長ずつ)読み込んでいけば
「000=A」「011=D」「001=B」…と文字コードに合わせて簡単に復号化できます。
では、可変長符号の場合はどうでしょう。
1101110010011001000101111
可変長符号の場合は、○bitずつという区切り方では元の記号に戻すことができません。上の符号を最初に3bit読みこめば「110=A」となりますが、同じように次も3bit読み込むと「111」となり「合致する記号なし」と判断されてしまいます。
ではどうするのか。実はハフマン符号化をした時点でこの問題は解決済みです。
ハフマン符号のすごいところは、各記号に対する符号化で「全く同じビットの並びが存在しない」ような符号化をするというところです。
| 文字 | 固定長符号 | 可変長符号 |
|---|---|---|
| B | 001 | 0 |
| C | 010 | 10 |
| A | 000 | 110 |
| D | 011 | 1110 |
| E | 100 | 1111 |
復号化する際は左から順に符号を読み取っていきます。上のデータの場合、最初に読み込む符号は「1」ですね。では、この1から予測される元の記号はなんでしょうか。「C」「A」「D」「E」になりますね。では2bit目・3bit目と読んでいってみてください。3bit目で「110」が読み取られ「110=A」が合致し確定しますね。
ハフマン符号では、この途中で元の記号以外の符号パターンが存在しないような符号化をするのです。
例えば、仮に「110=A」「11=B」という符号化をしてしまったとします。すると、「110=A」を求める前に2bit目で別の記号と合致するようなパターン、つまり「11=B」が出現してしまいます。ここで復号をしてしまうと、次に読み込まれるのは「0」からになってしまい、1つ左にずれてしまいます。これでは以降正しく復号化することができなくなってしまいます。
しかし、ハフマン符号化をした場合はこのような事態には絶対になりません。
これは、ハフマン木と呼ばれるツリー構造を作ったからです。ツリー構造を作ると、木の葉へ向かって曲がることで、接点に割り振られているビットとは逆のビットが割り振られるためです。
なので、ハフマン符号を復号するためには「○bitずつ」という制限で読み込むのではなく「順にビット列を読み込んでいって、一番最初に合致した記号で復号する」とやっていけば元の記号へ戻すことができます。
1101110010011001000101111
左から順に、最初に合致した記号で複合します。
最初は「110=A」が合致する、次は「1110=D」が合致、次は「0=B」が合致…と順に合致した記号で戻していけば正しく復号できます。
このように、符号の切れ目が無くとも順に読み込んでいけば正しく復号できる符号を「瞬時復号可能な符号」といいます。ハフマン符号は瞬時復号可能な符号のひとつです。
ハフマン符号は瞬時復号可能で一意の復号ができますので、コンパクト符号の条件に一致します。
まとめ
いかがでしたでしょうか。データ圧縮の基本のひとつ「ハフマン符号化」について解説しました。
「広く使われているから、さぞ難しいことをしているんだろうな~」と思っていた方も多いかと思いますが、このハフマン符号は結構理解しやすかったのではないでしょうか。
これを知ったからといって何かに役立つかと言われれば、プログラミングをしない限りは雑学で終わってしまいそうです。ですが、いつも自分が使っているJPEG圧縮やZIP圧縮の原理のひとつが理解できたことになります。
「なんで圧縮するとデータが小さくなるのに元のデータの情報は失わないのか?」という疑問を持った方は、この記事でその原理のひとつを知ったことになります。
今までの記事とは少し方向性が異なりましたが、この記事も何かお役になてたのならば幸いです。
- 2021年2月27日:Cの固定長符号が間違っていたため修正
- 2019年1月14日:内容を少し追記・更新
- 2013年3月16日:初出








コメント
コメント欄を開く
コメント一覧 (14件)
大変分かりやすく参考になりました。
ありがとうございました。
非常にわかりやすい解説ありがとうございました。
一発で理解できました。m(_ _)m
コメントの返信が遅れて申し訳ございません。
お役に立てて良かったです。この記事で書いたハフマン符号化の図は一例で、他にもハフマン木の作り方は
いろいろあるので(基本は同じですが)、興味がある場合は一緒に調べてみると面白いかと思います。
分かりやすい解説でした。仕組みを理解する事はとても大切な事だと思っています。
コメントありがとうございます。
仕組みまで分かればトラブルがあっても自分で解決できることが増えるので
なるべく私としても「その操作の理由」までちょっとでも知っていてくれれば
役立つと思い色々周囲の友人にはその旨言っているのですが・・・
中々伝わりませんね~(笑
学校でもらったプリントでは、なかなか理解できなかったけど、このサイトで一発で理解できました。
ありがとうございました。
文系学生なのに、情報系の授業を取ってしまってすごく困ってました。このサイトを見てやっと分かりました!ありがとうございます!!
管理人様
平成28年春期、高度情報(共通)の午前問題、第2問を解いていて、まったく解らなかったので、インターネットで解説を探し、貴ウェブサイトに出逢いました。
素晴しく解りやすい説明であり、解説の要点を書き写しながら読み進めた処、一遍で理解し終えました。更に復号の知識まで身に付いたので、今後は同種の問題を難なく正答し得る程です。
まことに有難う御座いました。
これから圧縮技術について教本・解説本などで勉強して行こうと思う素人です。PCスキルは中堅!
解説内容は解かり易いのですが、1つ疑問が生まれた。
それは、PC上では{符号化の伴う対応表}はデータ圧縮処理の際に、何処に有るのか?
デコード(復元)する場合、対応表がなければならないのではないのか?(圧縮データ本体に付加されてるのか?)
動画のデータ解析した対応表のデータは大きいと思う。
様々なFile形式[ MP3,AAC,WMA,FLAC,OGG,Mpeg2,Mpeg4,JPEG,ZIP…etc]が存在するが各々ハフマン符号の様な方式で圧縮・復元を行っているのでしょうか?
コメントありがとうございます。
私も専門に勉強したわけではないので概要くらいまでしかわかりませんが・・・
ハフマン符号化によるデコードは、圧縮の際に作成した符号情報のテーブルが必要になります。静的ハフマンではこのテーブルが必須です。圧縮計算中の表作成は主にメモリ上で行われ、終わったら書き出します。(これに限らずパソコンのデータ処理は主にメモリ上で行われますね。)
基本的にはこの符号テーブルは圧縮したデータの中に入っています。デコードする際にこのテーブルをメモリ上に展開して計算させれば複合できます。問題点として、確かにデータによってはうまく圧縮できず符号表付加によるオーバヘッドの問題がでてきます。
因みにですが、動的ハフマン(適応型ハフマン)の場合はこのテーブルなくてもよいみたいです。ただ、内容が難解で私には仕組みがよくわからなかったです・・・
一応、技術的なお話が載っているサイトを1つご紹介します。
●ハフマン符号化 – 適応型ハフマン圧縮
http://fussy.web.fc2.com/algo/compress4_ahc.htm
静的ハフマンの方が概要がわかりやすいので当記事ではこちらを紹介しています。実際、ZIPやPNGなどで利用されているdeflateというアルゴリズムは静的ハフマンの方を利用しているようです。
ハフマン符号というのは可逆圧縮のひとつで、エンコード後のデータからデコード処理によって元通りのデータを復元できる圧縮方法です。ただ、全データを単純にハフマン符号しているということは稀だと思います。お気づきの通り、全データをハフマン符号化しようものなら対応表のみでかなりのデータ量になるので全く圧縮になっていません。
なのでテーブル自身が大きくならないよう工夫が必要になります。どの部分のデータをどういった形で利用すればテーブルの肥大化を防ぐことができるのか。様々な処理がされている中、ハフマン符号化が最適だと思う所に処理を入れます。
例えば、JPEGでは画素のデータそのまま符号化しているわけではありません。その画素データの値を表すのに必要なビット数のみをハフマン符号化させています。こうすれば使う文字数が格段に減るので対応表も極端に大きくなりません。また、ハフマン符号化だけでなくランレングス圧縮など他の圧縮方法も組み合わせて行います。
世の中には様々な圧縮方法があり、それぞれ適した利用場所で使っています。ハフマン符号のような可逆圧縮ではなく、データが元に戻らない非可逆圧縮という方法もあります。MP3などがそれで、音声データの中で人間が感知しずらいと思われるデータのみをカットさせることで音質の低下を抑えながらデータを大幅にカットしています。そうした処理の中で、データ的に偏りがある部分がでてきた、かつハフマン符号が得意そうな偏りであった、ではこの部分はハフマン符号化で圧縮してみよう、といった感じでMP3もハフマン符号を使っています。
符号化(エンコード)とは、信号やデータなどを一定の規則に則って目的に応じた別のデータへ変換することを指します。お書きいただいたようなファイル形式も、プログラムがエンコード処理をした結果として作られます。そして、伸張・展開・再生するためデータを元に戻すことができる「デコーダー」でデコードを行ないます。デコーダもプログラムですので、その規格に則って元に戻せるよう作成します。(因みに、エンコードとデコードが1つの装置、プログラムで実行できるものをコーデックと呼びます。)
例えば、JPEGはJIS規格としても定められており、「JISX4301」として閲覧が可能です。この中にデコード処理の方法も記載があるようです。私が見てもさっぱりでしたが(笑 (※サイト上で閲覧のみ、印刷等したい場合は別途購入。)
また、MP3などは確かに規格として圧縮方法などが決められていますが、1から10まできっちり決まっているわけではなく、ある程度圧縮方法を工夫できる余地があります。なので、MP3はエンコーダーによって作成されるデータが異なったりします。ただし、どのエンコーダーを利用してもMP3のデコーダーでしっかり戻せるように設計します。
いずれのデータも非常に複雑な処理がされておりますので「各々ハフマン符号の様な方式で圧縮・復元を行っている」わけではありません。そう単純ではなく、あらゆる方法を駆使し利用目的に沿って効率的に圧縮・復元しています。
では実装部分ではどうなのか、という点は私もそこまで勉強はしていないので、申し訳ございませんがまた実践的な部分は教本などで勉強されてみてください。
長くなりましたが、ご参考なりましたら幸いです。
とてもためになりました!すごく解りやすかったです。
とても分かりやすくありがとうございます!基本技術者情報試験の勉強をしていたので役立ちました^^
大変わかりやすく勉強になりました。
ありがとうございます!
⑤と⑥のCの固定長符号はあっていますか?
010では、と思っているのですが。
コメントありがとうございます。お役に立てたようでよかったです。
ご指摘いただきました部分の符号ですが、確かに途中から間違っていました。この記事では「C=010」と最初に定義していたのですが、途中でDのものと同じになってしまっていました。一列にまとめたときの符号は合っています。
ご迷惑をおかけして申し訳ございません。先ほど修正させていただきましたので、よろしければまたご確認いただけましたら幸いです。
お忙しい中、ご指摘のコメントありがとうございました。